GO BACK
| Note on the theory of
regularity structures |
|
Chapter 1
Algebraic renormalisation of
regularity structures
This chapter is taken from the paper [Y. Bruned, M. Hairer, L. Zambotti,
Invent. Math. 215 (2019), no. 3, 1039–1156].
1.1Rooted forest
1.2Bigraded spaces and
triangular maps
1.3Incidence
coalgebras of forests
-
 . Denote by
. Denote by  the free vector space generated by
the free vector space generated by  .
. 
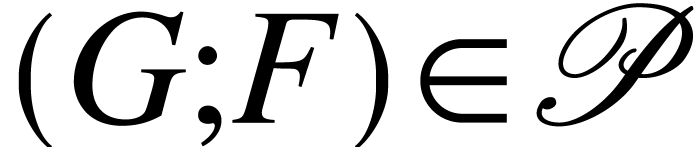 we are given a (finite) collection
we are given a (finite) collection 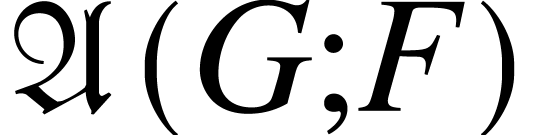 of
subforests
of
subforests  of
of  s.t.
s.t.
 . Define
. Define 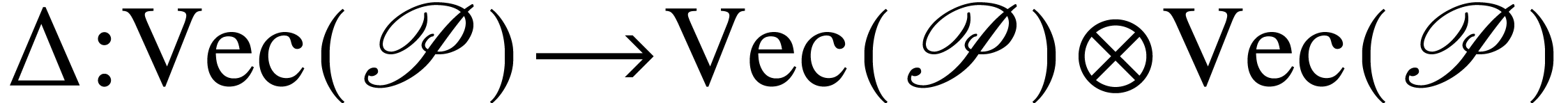 by
by
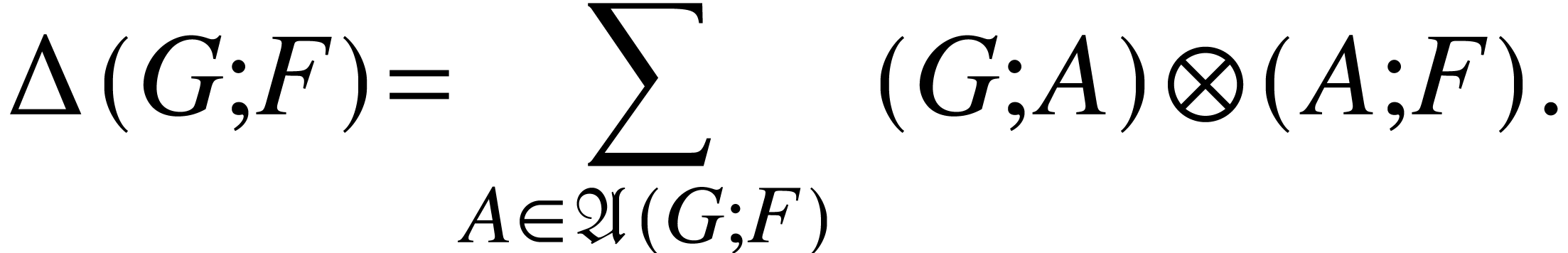
Define the linear functional  by
by 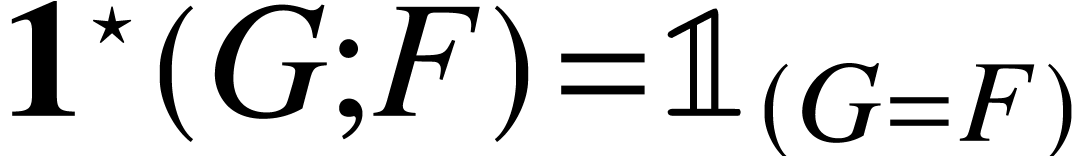 . If
. If 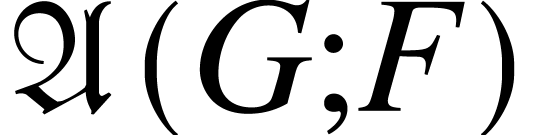 is equal to all subforests
is equal to all subforests  of
of  containing
containing  ,
then
,
then 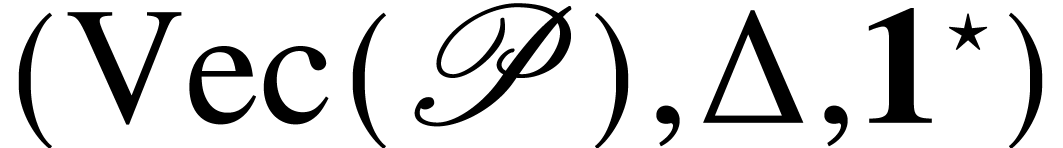 is a coalgebra. Since the inclusion
is a coalgebra. Since the inclusion
 endows the set of typed forests with
partial order,
endows the set of typed forests with
partial order, 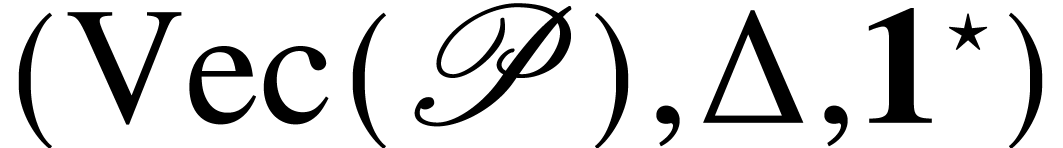 is an example of an
incidence coalgebra.
is an example of an
incidence coalgebra.
-
Given a typed forest  ,
consider a several disjoint subforest
,
consider a several disjoint subforest 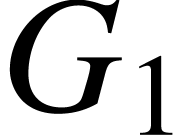 ,
, 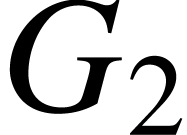 ,
, ,
, 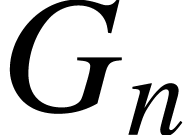 of
of
 . A natural way to code
. A natural way to code
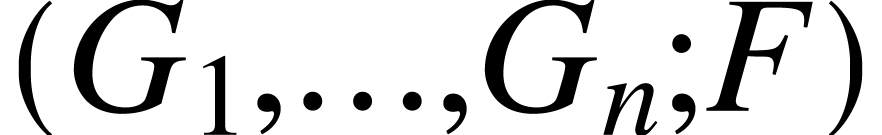 is to use a coloured forest
is to use a coloured forest 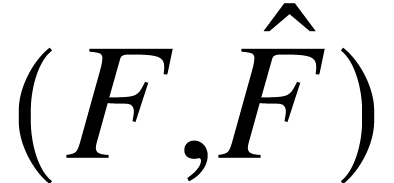 where
where
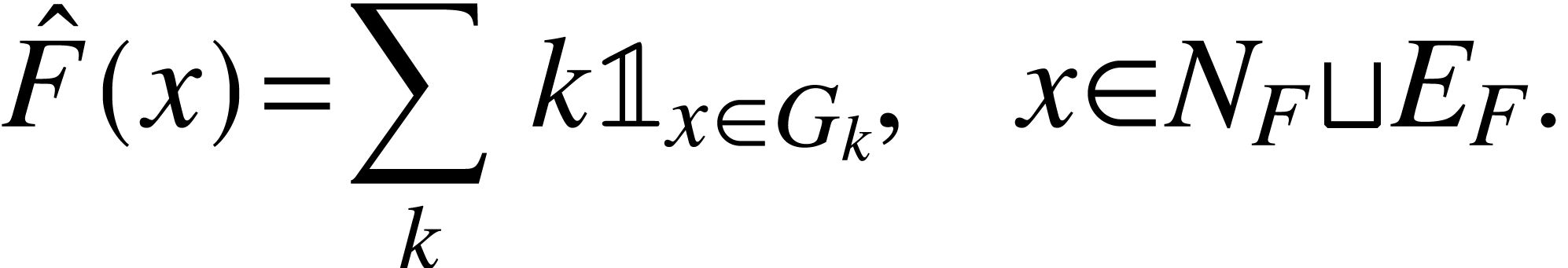
Then we have 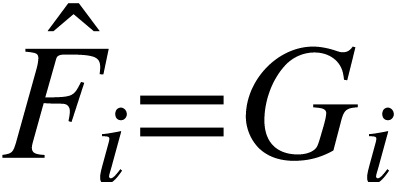 for
for  and
and 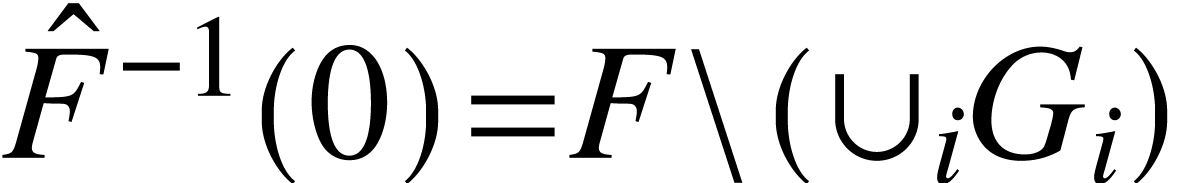 .
.
-
Assumption 1. Let  .
For each colour forest
.
For each colour forest 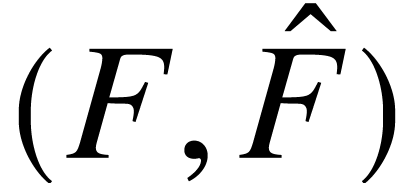 ,
we are given a collection
,
we are given a collection 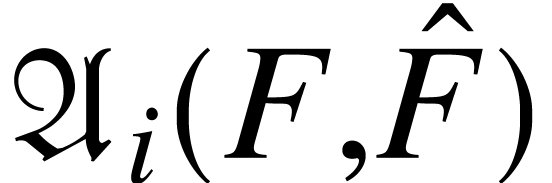 of subforests of
of subforests of
 s.t.
s.t. 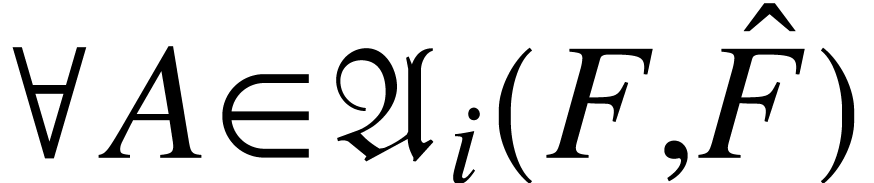
-
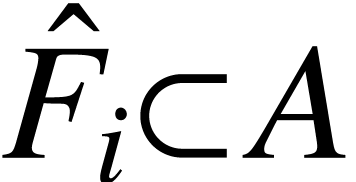 &
& 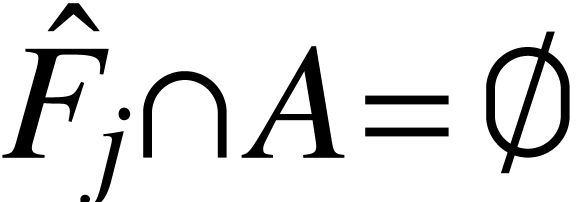 ∀
∀ ,
,
-
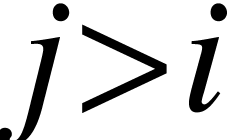
 ,
,  connected component
connected component  of
of 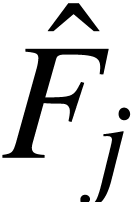 , one has either
, one has either  or
or 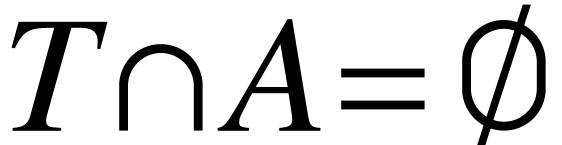 .
.
We also assume that  is compatible with
forest isomorphisms described above in the sense that
is compatible with
forest isomorphisms described above in the sense that

Chapter 2
Phi-four equation in the full
sub-critical regime
In this chapter, we consider the  equation in the
full sub-critical regime. The equation is formally given by
equation in the
full sub-critical regime. The equation is formally given by

where the term  represents the renormalisation
(it can be quadratic in
represents the renormalisation
(it can be quadratic in  ) and
the noise
) and
the noise 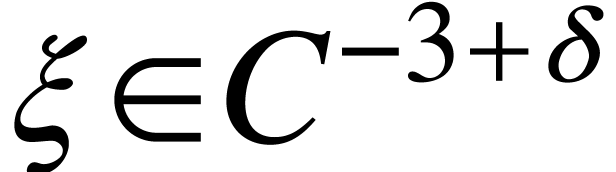 for some
for some 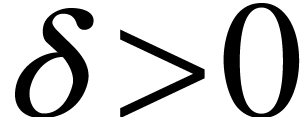 .
This chapter is a note taken from the paper [A. Chandra, A. Moinat, H.
Weber, Arch. Ration. Mech. Anal. 247 (2023), no. 3, Paper No. 48].
.
This chapter is a note taken from the paper [A. Chandra, A. Moinat, H.
Weber, Arch. Ration. Mech. Anal. 247 (2023), no. 3, Paper No. 48].
2.1Preliminaries
We introduce the following ingredients.
Appendix A
Basic Hopf
algebras
This note is extended from the a course called MAGIC 109 given by Dr Y.
Bazkov, adding some materials from the following resources:
-
M. E. Sweedler. Hopf algebras, Math. Lecture Note Ser. W. A.
Benjamin, Inc., New York, 1969, vii+336 pp.
A.1Informal introdution
A.1.1Example – Symmetries
on the real line
We intend to study the intrinsic geometric property of the real line
 by looking at how functions on the real line can
transform. For more algebraic setting, we only consider polynomials over
real variable. Let us look at the following transforms.
by looking at how functions on the real line can
transform. For more algebraic setting, we only consider polynomials over
real variable. Let us look at the following transforms.
Given a real number  and
and 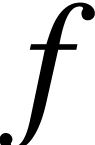 is a function on the real line, we define the following translation
by
is a function on the real line, we define the following translation
by  :
:
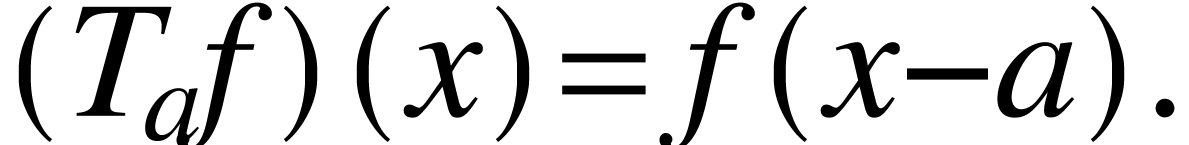
Define also the reflection
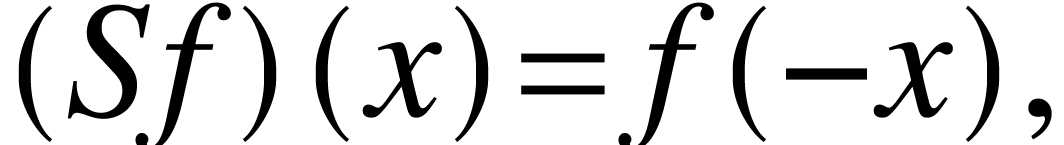
and the derivative
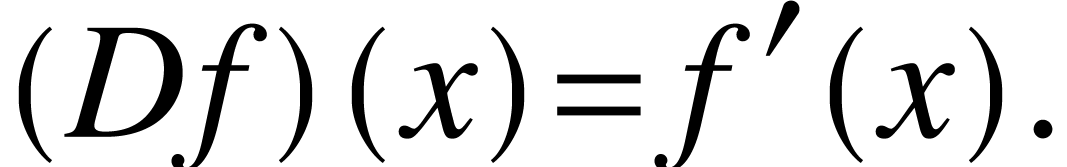
The translation, reflection, derivative are not independent from each
other. In fact, there are some relations:
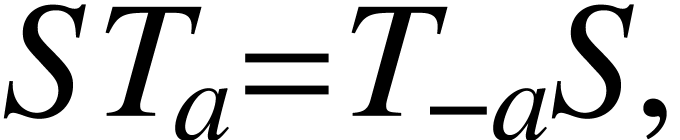 |
(A.1.1) |
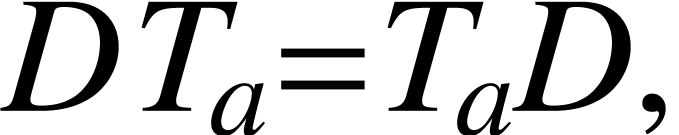 |
(A.1.2) |
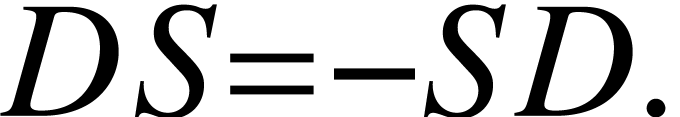 |
(A.1.3) |
Proof of (A.1.1). 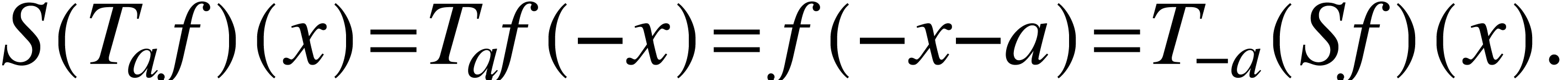

Also,
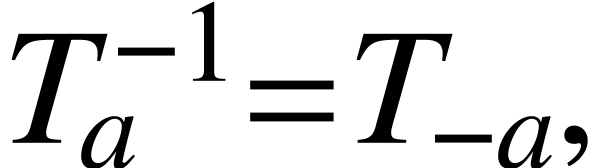 |
(A.1.4) |
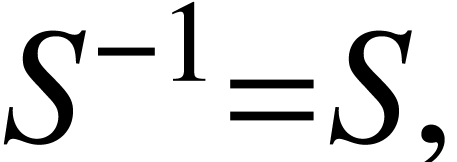 |
(A.1.5) |
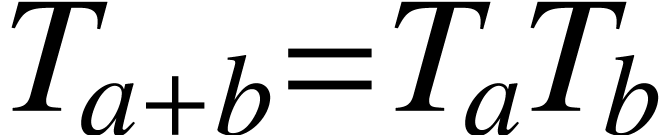 |
(A.1.6) |
Now we write down the relation (A.1.1)-(A.1.2)-(A.1.3)-(A.1.4)-(A.1.5)-(A.1.6)
for 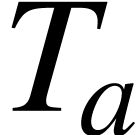 ,
, 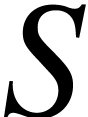 , and
, and 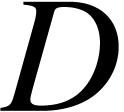 ,
so these transformations live their own lifes without the mention of the
functions they act on. But the algebraic structure given by (A.1.1)-(A.1.2)-(A.1.3)-(A.1.4)-(A.1.5)-(A.1.6) is too “blank”, it does not contain enough
information for us to effectively work with these abstract symbols as
symmetries of the function space on the real line. What is missing here
is how the operators
,
so these transformations live their own lifes without the mention of the
functions they act on. But the algebraic structure given by (A.1.1)-(A.1.2)-(A.1.3)-(A.1.4)-(A.1.5)-(A.1.6) is too “blank”, it does not contain enough
information for us to effectively work with these abstract symbols as
symmetries of the function space on the real line. What is missing here
is how the operators 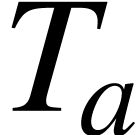 ,
, 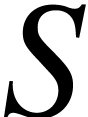 , and
, and 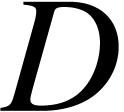 behave when we apply them to a product of functions. Given functions
behave when we apply them to a product of functions. Given functions
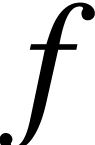 and
and 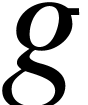 ,
,
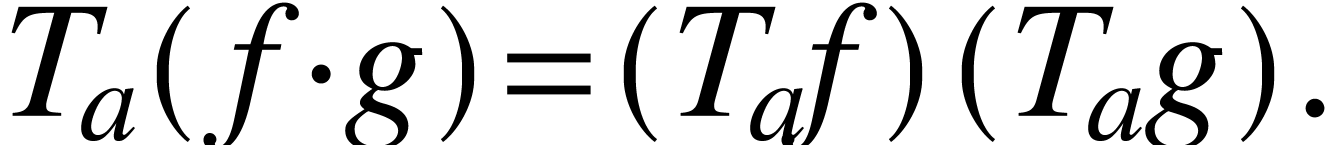 |
(A.1.7) |
To get rid of the mention of 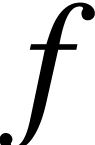 and
and 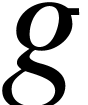 in (A.1.7), we introduce a new symbolic
notation coproduct
in (A.1.7), we introduce a new symbolic
notation coproduct  ,
satisfying
,
satisfying
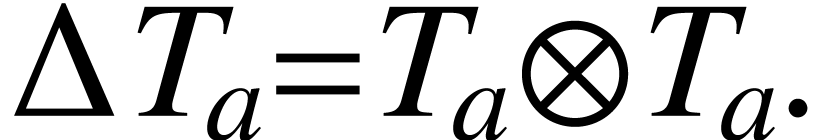
Likewise, we also require
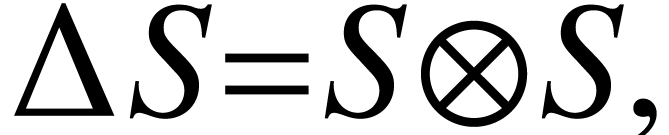
and the Leibniz rule
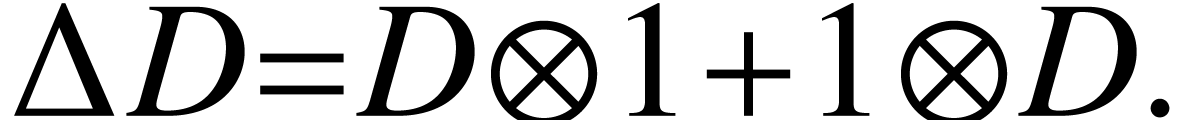
The meaning of  will become clear later in this
note.
will become clear later in this
note.
A.1.2Hopf algebra –
informal introduction
A Hopf algebra  , roughly
speeking, is a collection of operators which has
, roughly
speeking, is a collection of operators which has
-
rules for multiplication (i.e., how to compose operators);
-
rules for coproduct (i.e., how an operator acts on a product of
functions);
-
rules for The Antipode (roughly an analogue of inverse in
group).
In the example we study in Subsection A.1.1, we say that
the operators 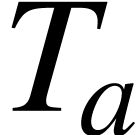 ,
, 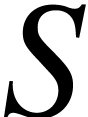 , and
, and 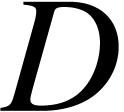 generate some
Hopf algebra. However, these operators are known even from 19 centrary,
what is the point to rename them? Hopf algebras gain an advantage over
groups when we need symmetries of a noncommutative space. The
noncommuting objects upon which we want to act can be thought of as
“functions” on a mythical “quantum group”.
generate some
Hopf algebra. However, these operators are known even from 19 centrary,
what is the point to rename them? Hopf algebras gain an advantage over
groups when we need symmetries of a noncommutative space. The
noncommuting objects upon which we want to act can be thought of as
“functions” on a mythical “quantum group”.
A.2Linear algebra
We consider vector space 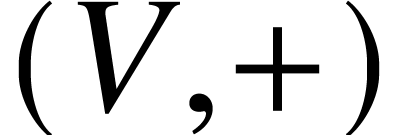 over field
over field  (sometimes we might use
(sometimes we might use  or
or  ). Recall that a linearly
independent set
). Recall that a linearly
independent set  is such that for any
is such that for any 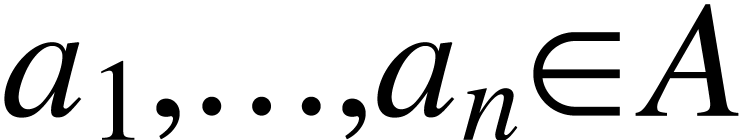 ,
, 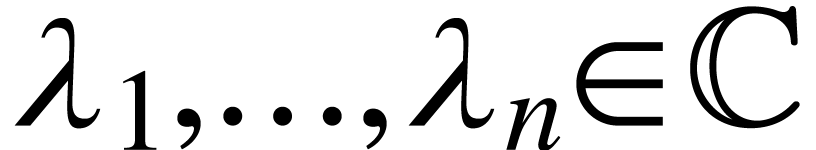 ,
,
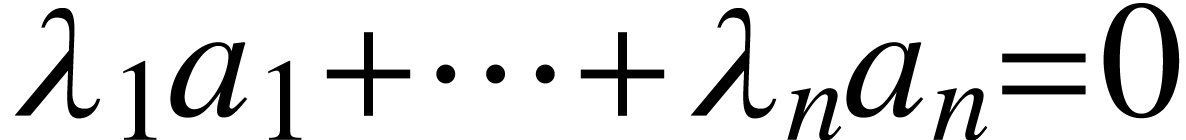 implies
implies 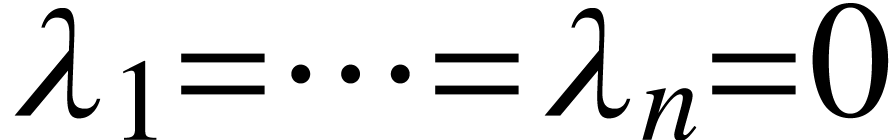 .
Given a subset of
.
Given a subset of 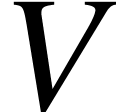 , say
, say  , the span of
, the span of  is defined by
is defined by 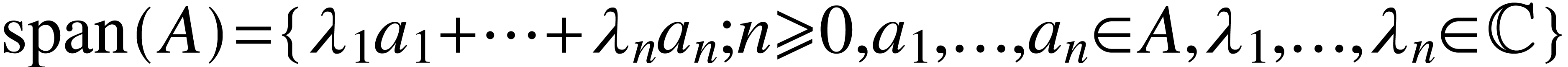 . A basis
. A basis  of
of 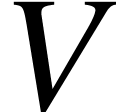 is linearly independent
subset of
is linearly independent
subset of  such that
such that  . By using Zorn's lemma, one can prove that every
vector space has a basis. All bases of
. By using Zorn's lemma, one can prove that every
vector space has a basis. All bases of 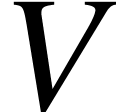 are of
the same cardinality which is denoted by
are of
the same cardinality which is denoted by 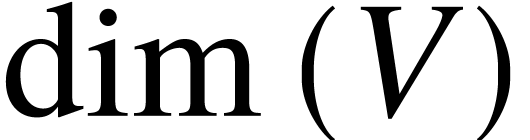 .
We can also argue that every set is a basis of some vector space.
Indeed, let
.
We can also argue that every set is a basis of some vector space.
Indeed, let 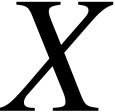 be a set, and let
be a set, and let
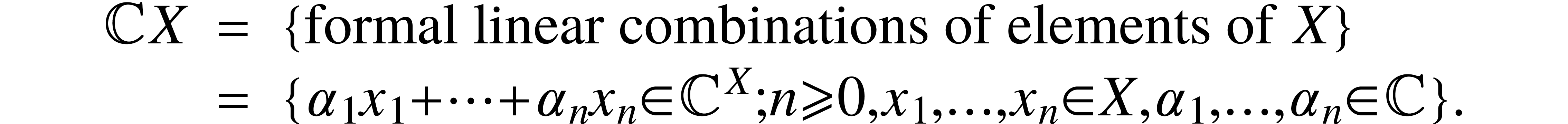
Moreover, we can identify 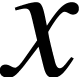 in
in 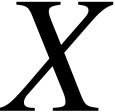 with an element in
with an element in 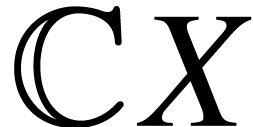 , which is
, which is
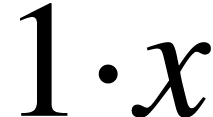 , and one can check that
under this identification the set
, and one can check that
under this identification the set 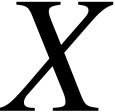 becomes a
basis of
becomes a
basis of 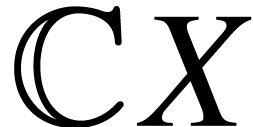 . This fits a
philosophy we have to adhere in this note: everything is vector space;
everything map is a linear map.
. This fits a
philosophy we have to adhere in this note: everything is vector space;
everything map is a linear map.
It is time to state the first result in this note, a result that we will
used later.
Proposition A.2.1. (linear extension from basis) Let  be a basis of vector space
be a basis of vector space 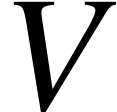 ,
, 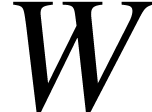 a vector space, and
a vector space, and 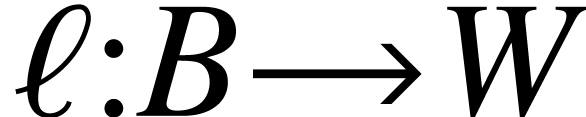 a function. Then there exists a unique linear map
a function. Then there exists a unique linear map
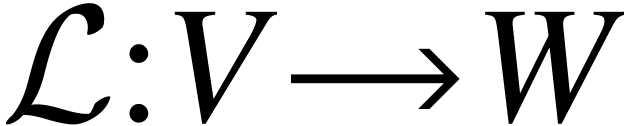 such that
such that 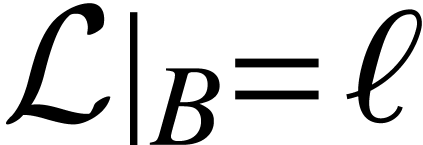 .
.
We will need a number of constructions which allows us to create new
vector spaces from the existing ones. For example, direct product and
direct sum of vector spaces  means
means
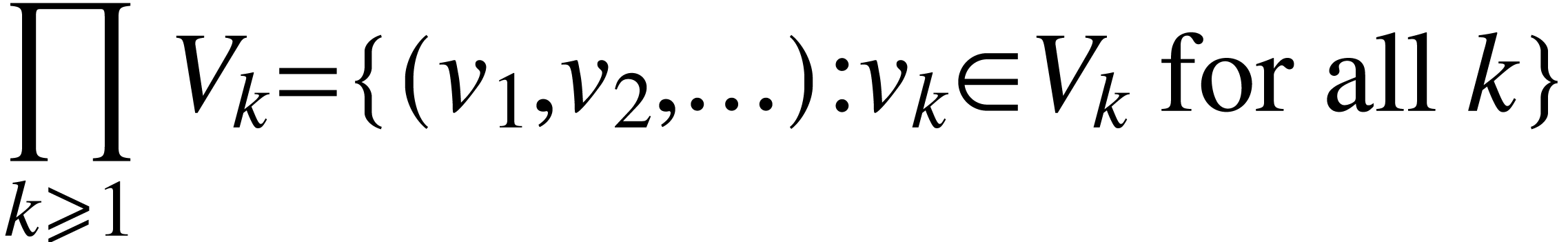
and
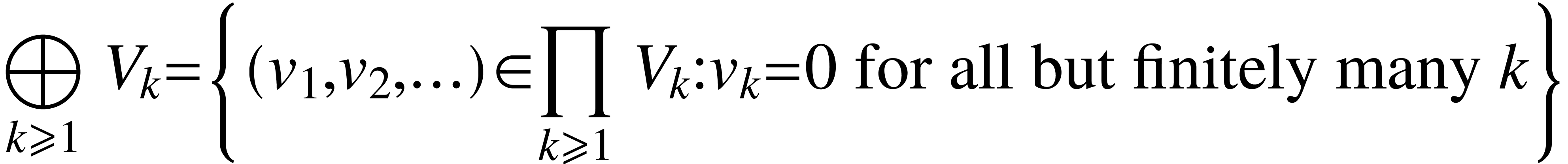
respectively. Let us note that for any 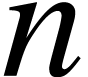 ,
,
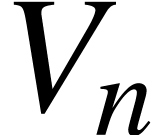 is a subspace of
is a subspace of 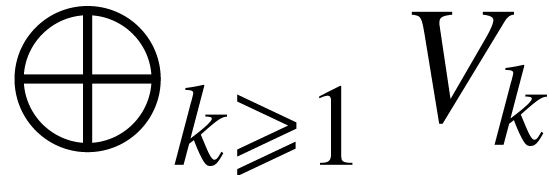 .
Let us also remark that direct product and direct sum can be defined for
an uncountable family of vector spaces. However, we only consider
countable familys in this note.
.
Let us also remark that direct product and direct sum can be defined for
an uncountable family of vector spaces. However, we only consider
countable familys in this note.
 is a finite connected simple
graph without circles with a distinguished vertex
is a finite connected simple
graph without circles with a distinguished vertex 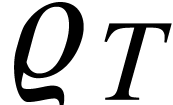 , called the root. We assume that
our trees are combinatorial, i.e. there is no particular order
imposed on edges leaving any given vertex.
, called the root. We assume that
our trees are combinatorial, i.e. there is no particular order
imposed on edges leaving any given vertex.
 is also called nodes. The
set of nodes of the tree
is also called nodes. The
set of nodes of the tree  is denoted by
is denoted by 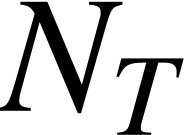 , and set of edges the tree
, and set of edges the tree
 is denoted by
is denoted by 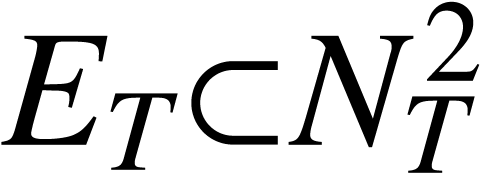 .
We endow
.
We endow 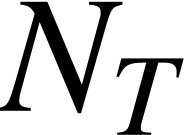 with the partial order
with the partial order 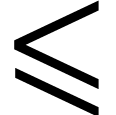 where
where 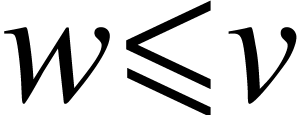 iff
iff  is on the unique path connecting
is on the unique path connecting 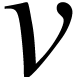 to the
root, and we orient edges in
to the
root, and we orient edges in  so that if
so that if
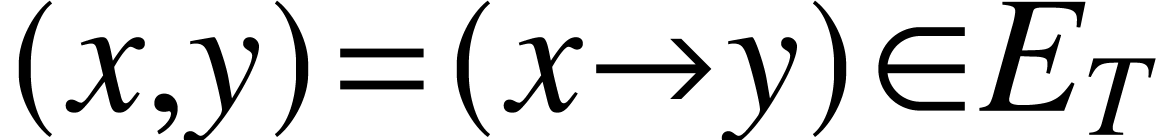 , then
, then 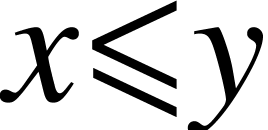 . In this way, we can always view a tree as
a directed graph.
. In this way, we can always view a tree as
a directed graph.
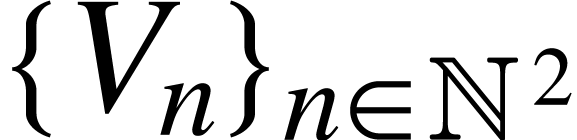 ,
,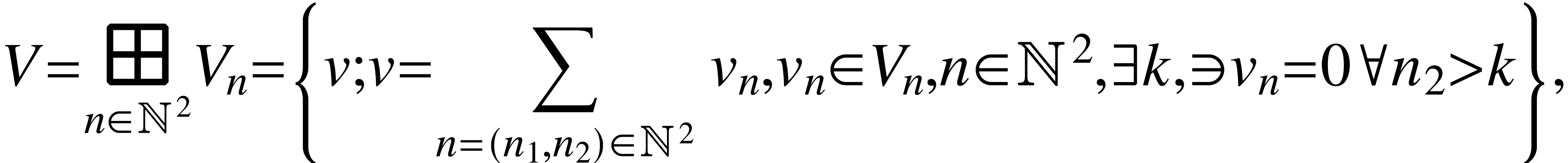
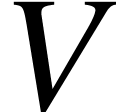 and
and  ,
,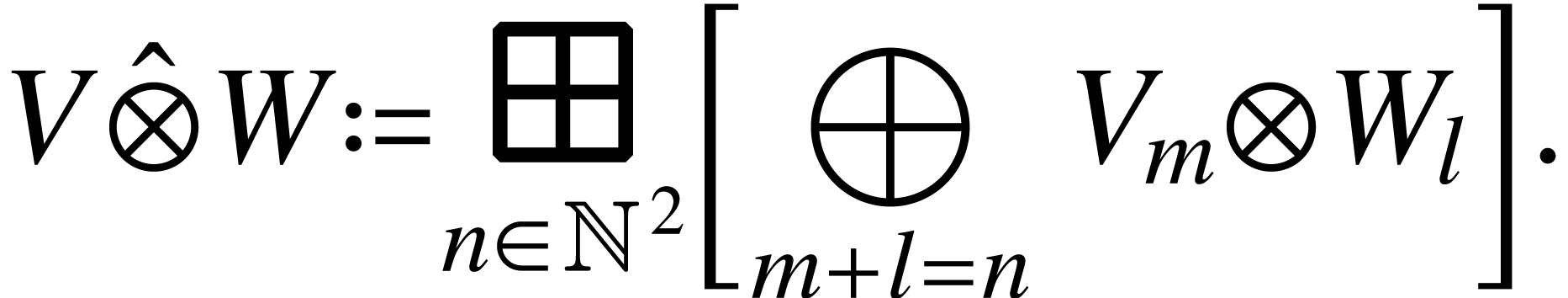
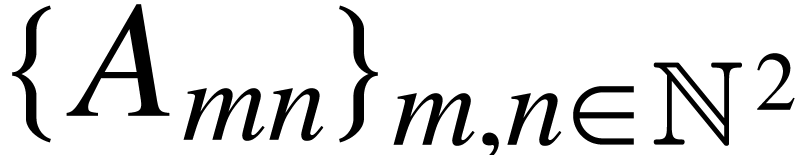 is s.t.
is s.t. 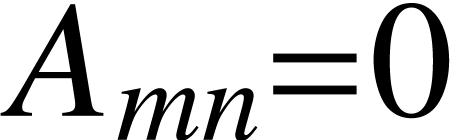 unless
unless 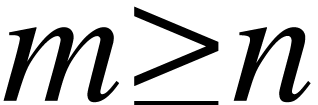 (i.e.
(i.e. 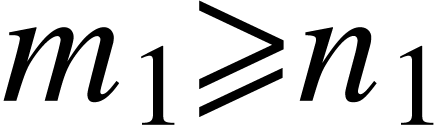 &
& 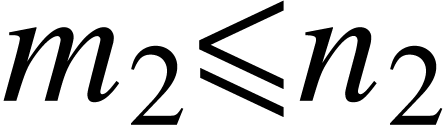 ).
).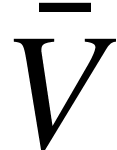 ,
,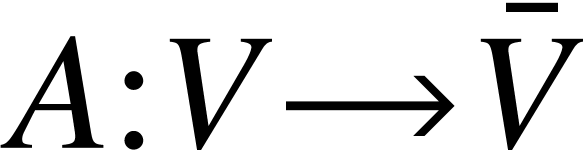 s.t.
s.t.
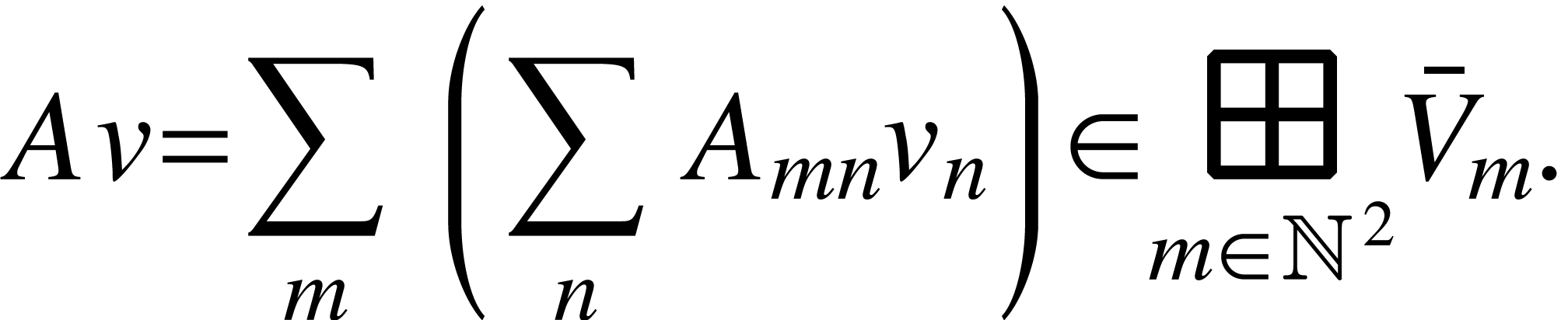
 can be view as a bigraded space with
can be view as a bigraded space with
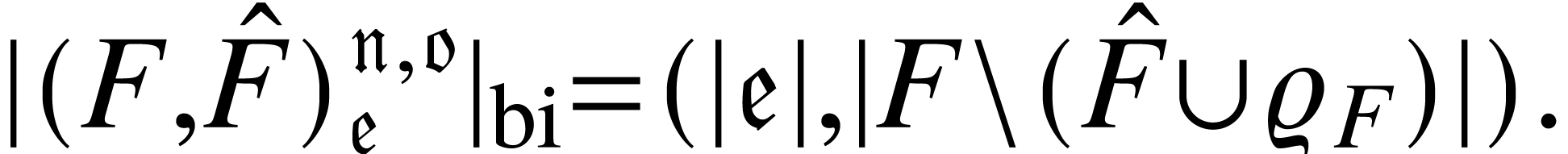
 .
.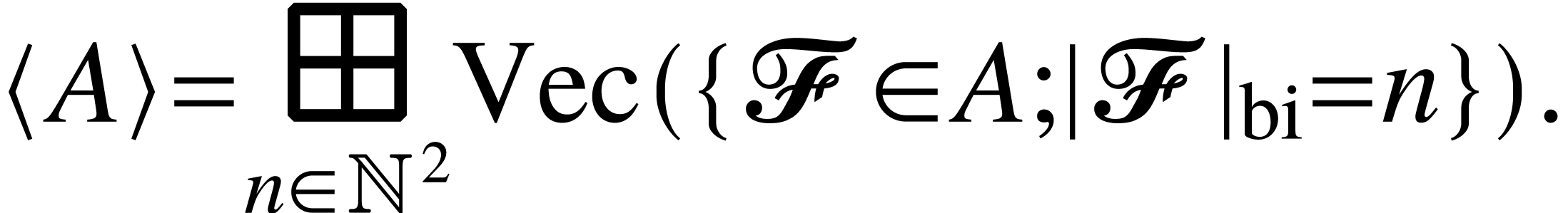
 .
. the free vector space generated by
the free vector space generated by  .
.
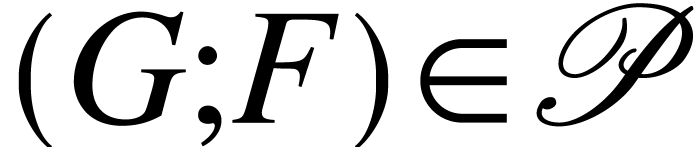 we are given a (finite) collection
we are given a (finite) collection 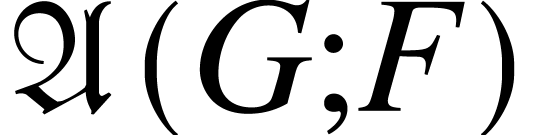 of
subforests
of
subforests  of
of  s.t.
s.t.
 .
. by
by
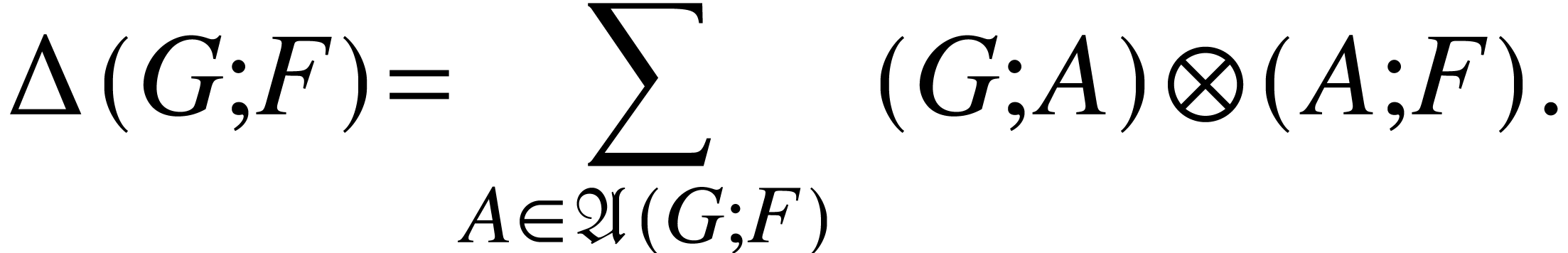
 by
by 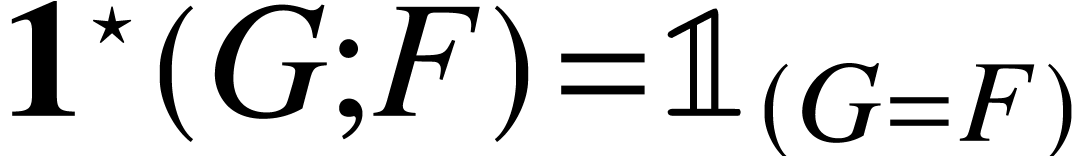 .
. ,
,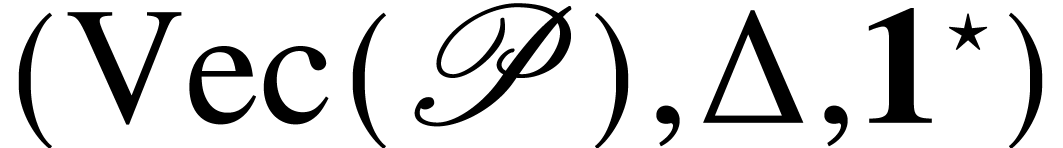 is a coalgebra. Since the inclusion
is a coalgebra. Since the inclusion
 endows the set of typed forests with
partial order,
endows the set of typed forests with
partial order,  ,
, ,
, ,
,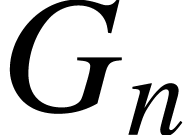 of
of
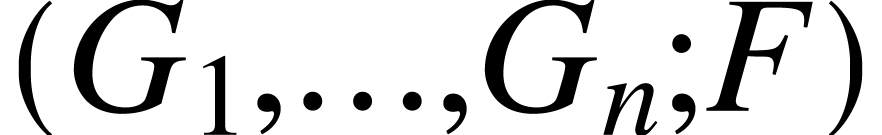 is to use a coloured forest
is to use a coloured forest 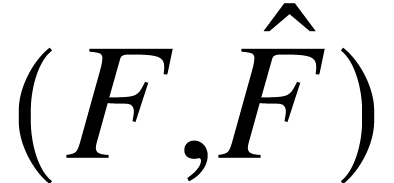 where
where
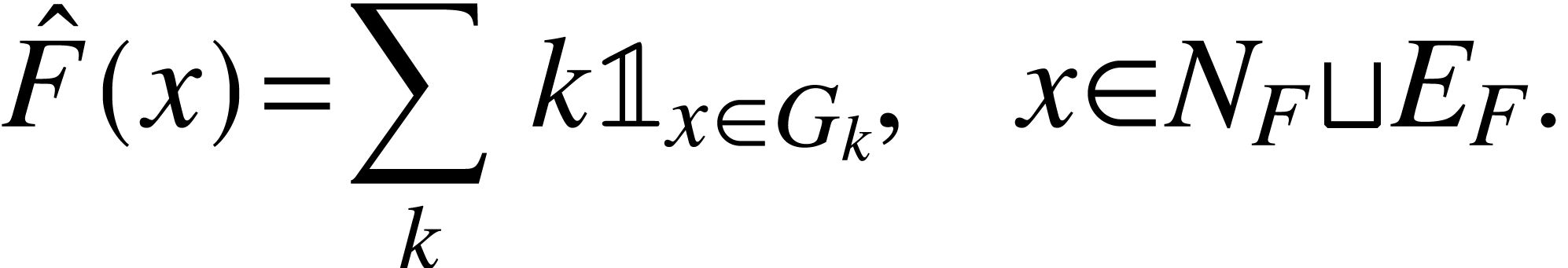
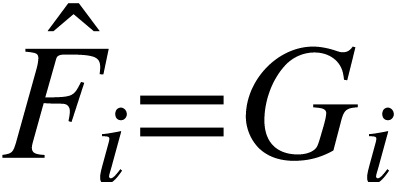 for
for  and
and 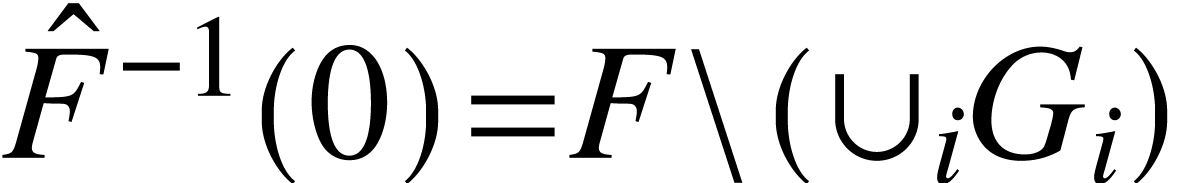 .
. ,
, of subforests of
of subforests of
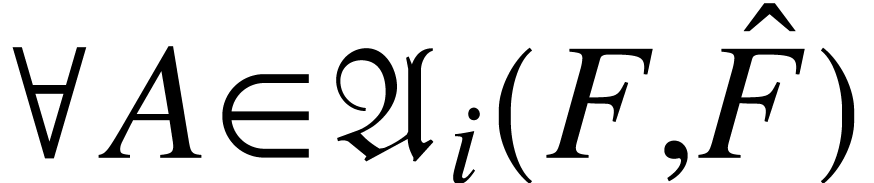
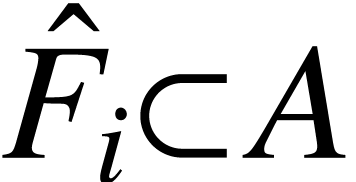 &
& 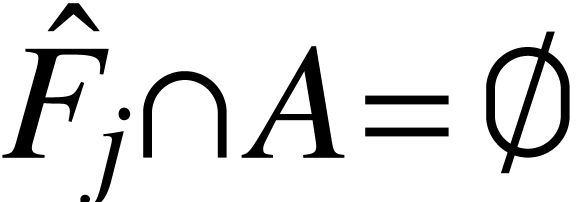 ∀
∀ ,
, ,
,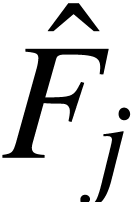 ,
, or
or 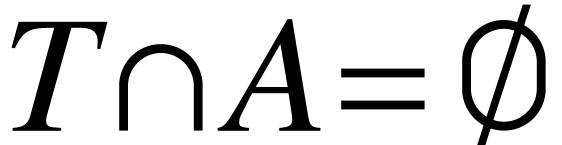 .
. is compatible with
forest isomorphisms described above in the sense that
is compatible with
forest isomorphisms described above in the sense that

 equation in the
full sub-critical regime. The equation is formally given by
equation in the
full sub-critical regime. The equation is formally given by

 represents the renormalisation
(it can be quadratic in
represents the renormalisation
(it can be quadratic in  )
) for some
for some 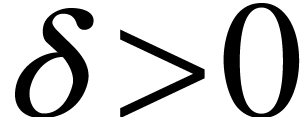 .
.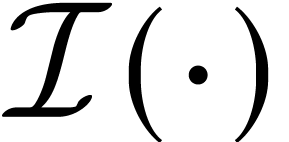 to represent an abstract Duhamel
operator for heat equation.
to represent an abstract Duhamel
operator for heat equation.
 be the smallest set containing the
symbols
be the smallest set containing the
symbols  s.t. “
s.t. “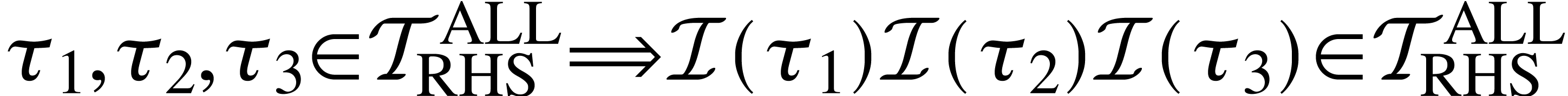 ”.
”.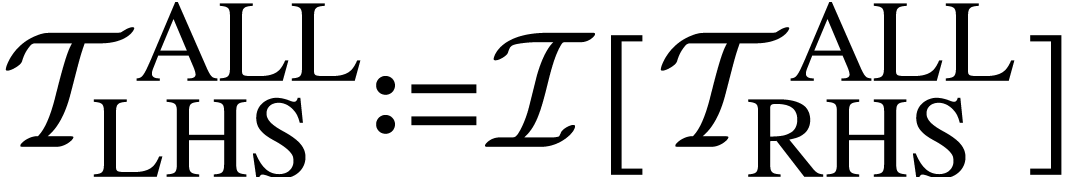 .
. to indicate elements in
to indicate elements in  .
.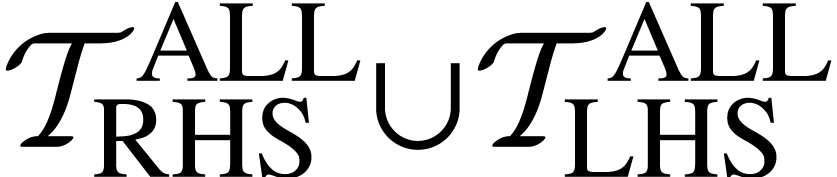 trees. In a given
tree,
trees. In a given
tree,  occur in that tree are called leaves
in the tree.
occur in that tree are called leaves
in the tree.
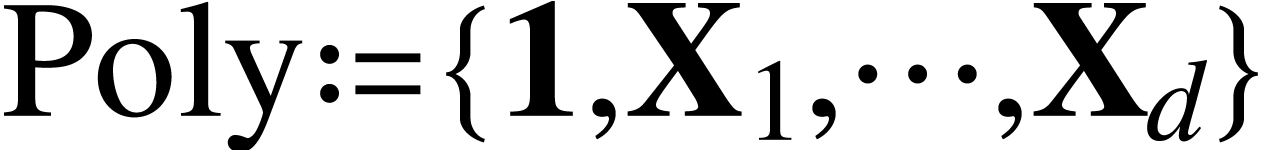 .
.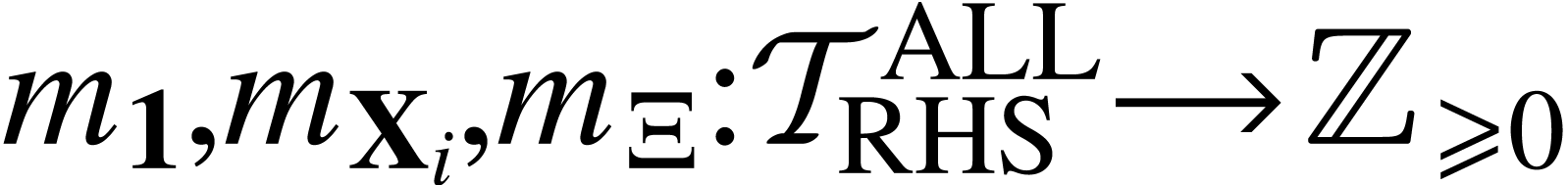 which counts, on any given
tree, the number of occurrences of
which counts, on any given
tree, the number of occurrences of 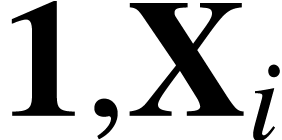 ,
, as leaves in the tree. Denote also by
as leaves in the tree. Denote also by
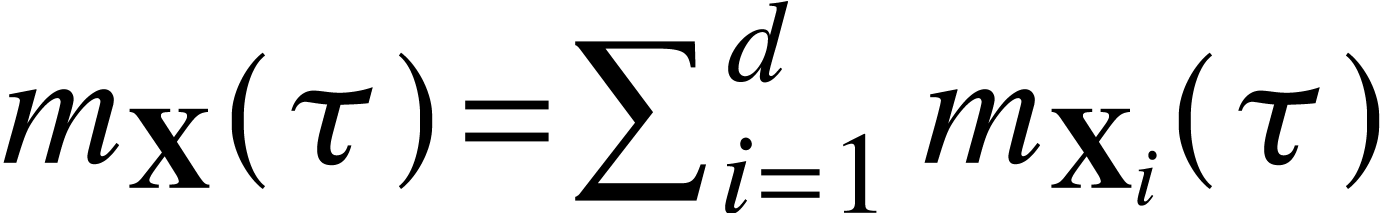 .
.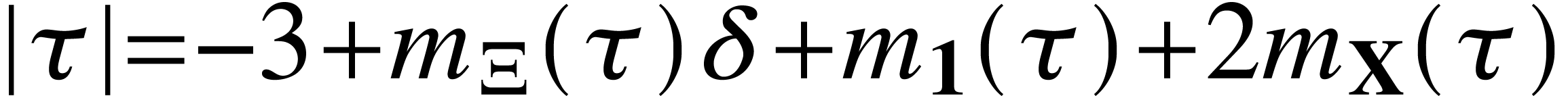 .
. ,
,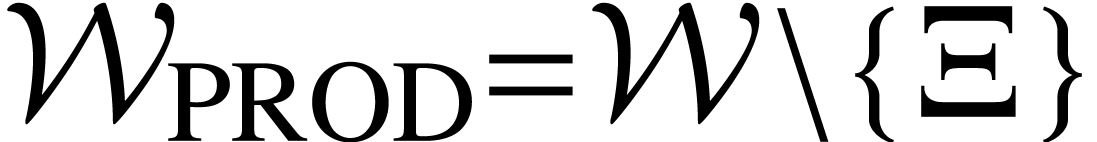 ,
, ,
,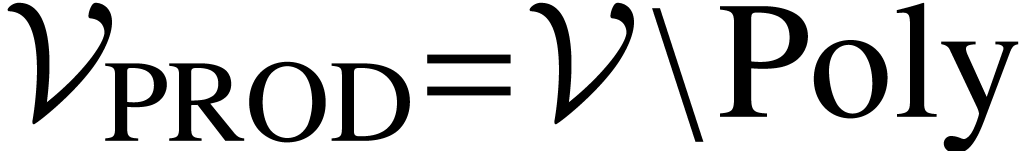 .
.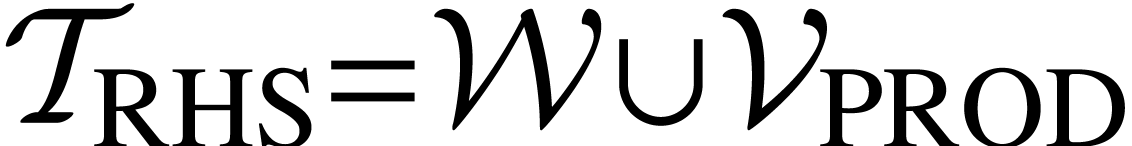 ,
,
 consists of
consists of 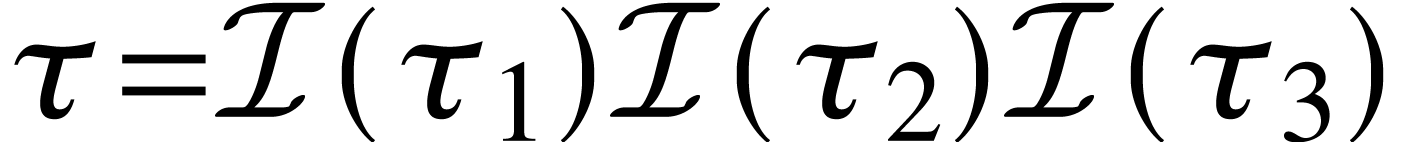 s.t.
s.t.
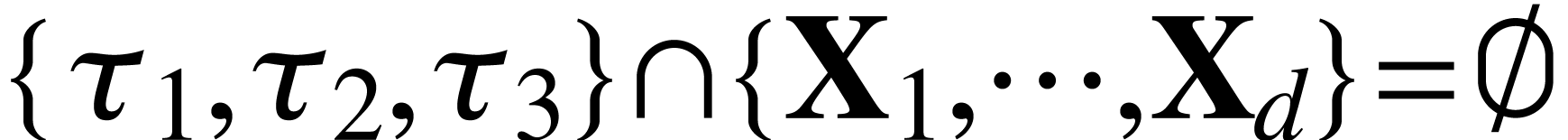 and
and 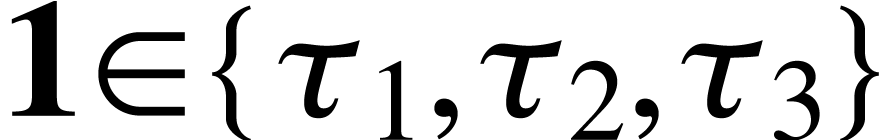 .
. .
.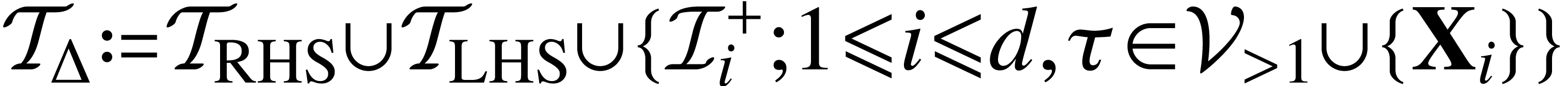 .
.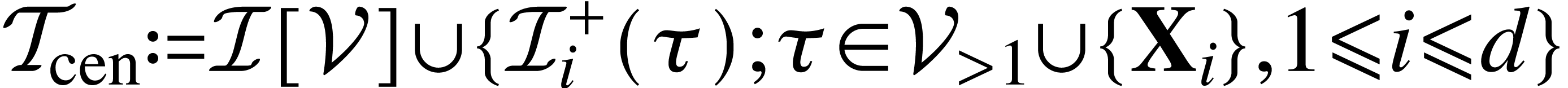 .
.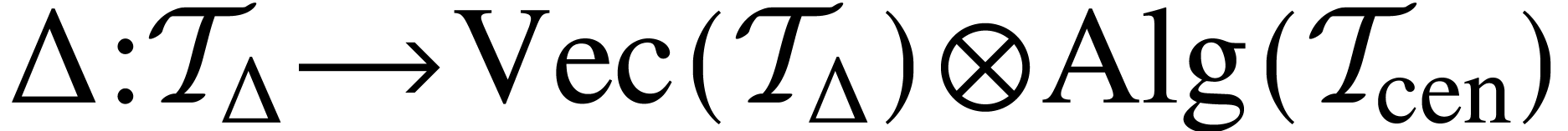 .
.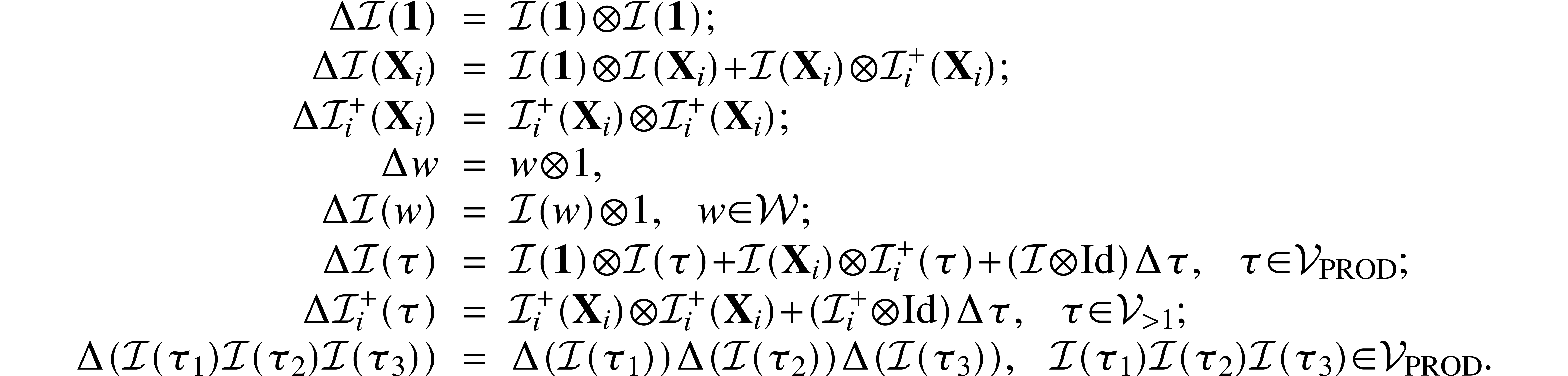
 by looking at how functions on the real line can
transform. For more algebraic setting, we only consider polynomials over
real variable. Let us look at the following transforms.
by looking at how functions on the real line can
transform. For more algebraic setting, we only consider polynomials over
real variable. Let us look at the following transforms.
 and
and 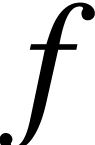 is a function on the real line, we define the following translation
by
is a function on the real line, we define the following translation
by 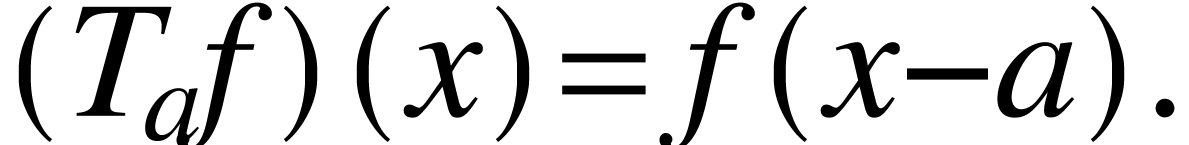
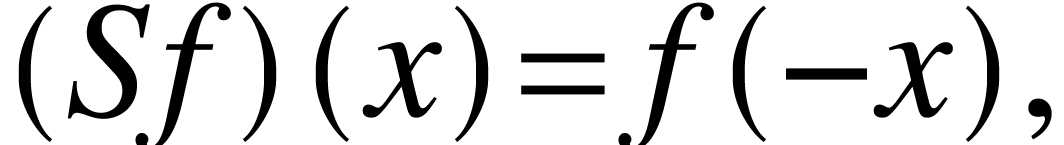
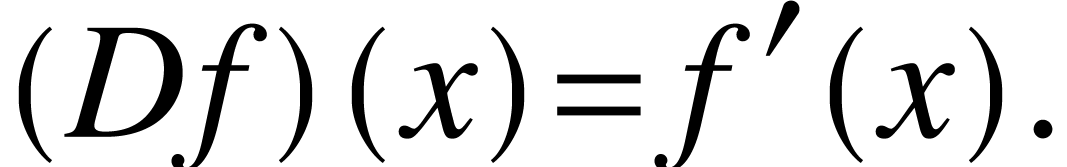
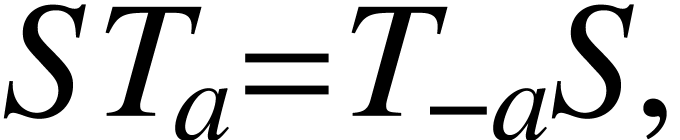
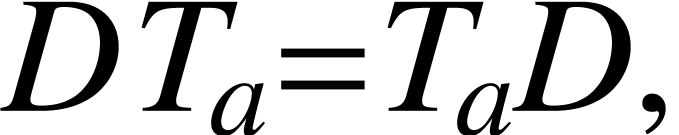
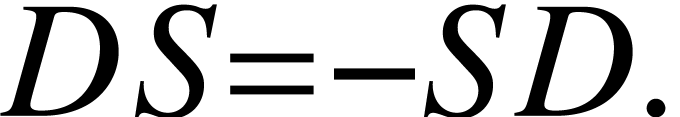
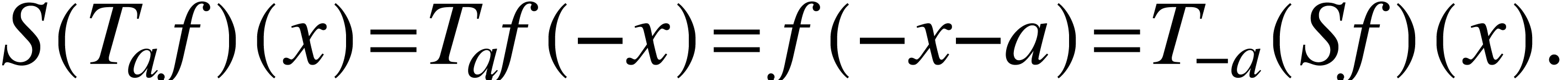

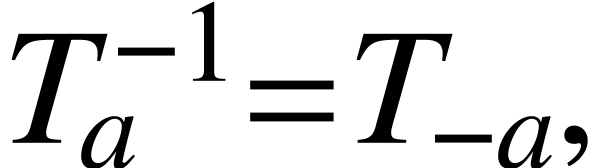
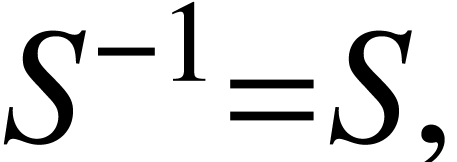
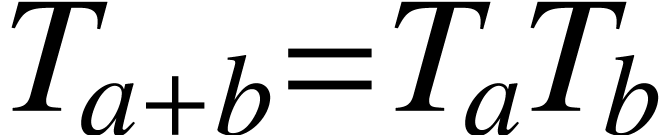
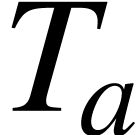 ,
,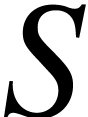 ,
,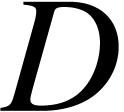 ,
,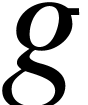 ,
,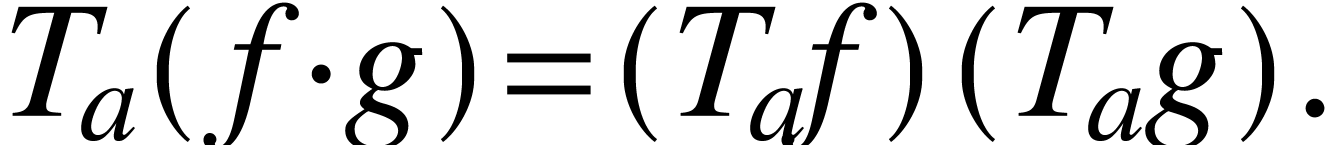
 ,
,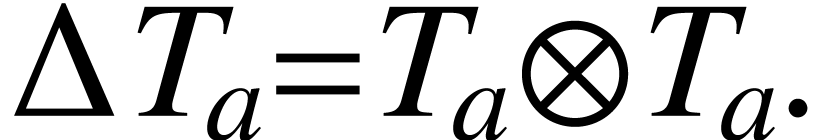
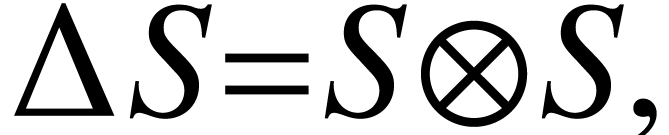
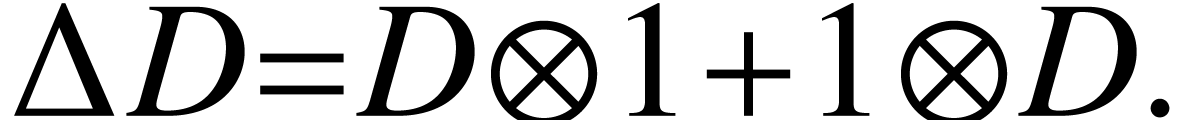
 ,
,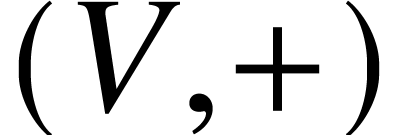 over field
over field  (sometimes we might use
(sometimes we might use  ).
). is such that for any
is such that for any 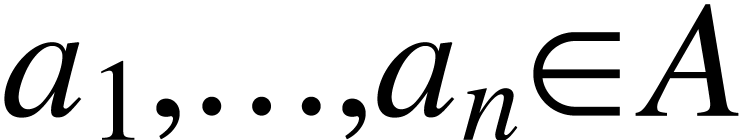 ,
,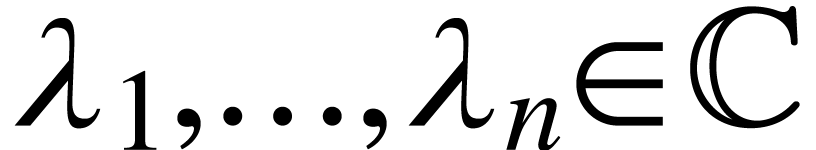 ,
,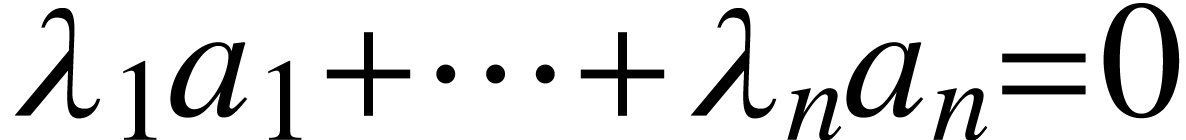 implies
implies 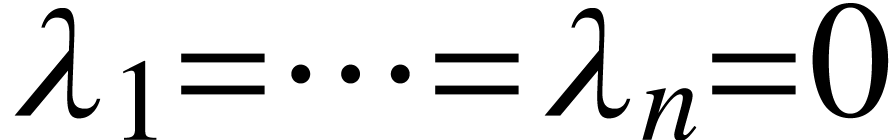 .
.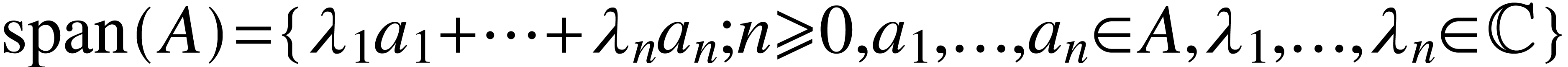 .
. of
of  .
.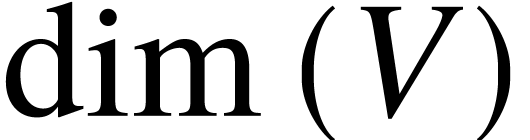 .
. be a set, and let
be a set, and let
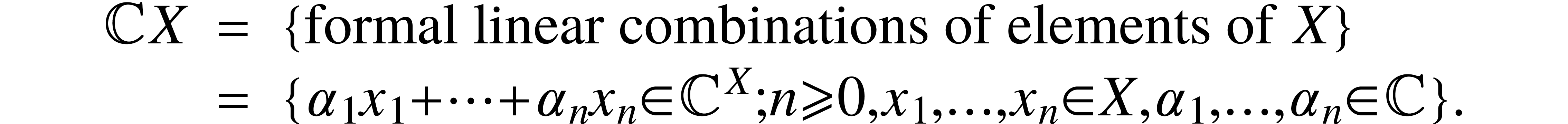
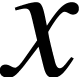 in
in 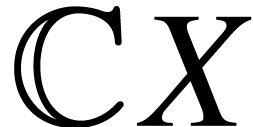 ,
,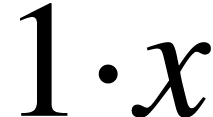 ,
, be a basis of vector space
be a basis of vector space 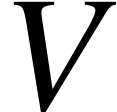 ,
,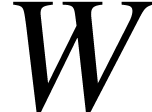 a vector space, and
a vector space, and 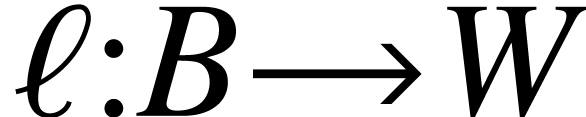 a function. Then there exists a unique linear map
a function. Then there exists a unique linear map
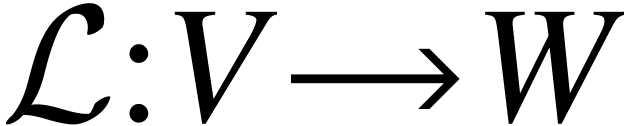 such that
such that 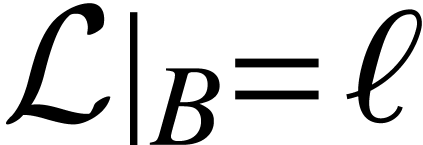 .
.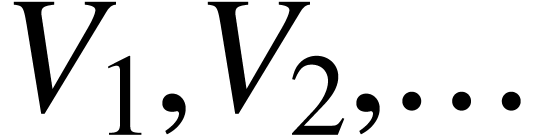 means
means
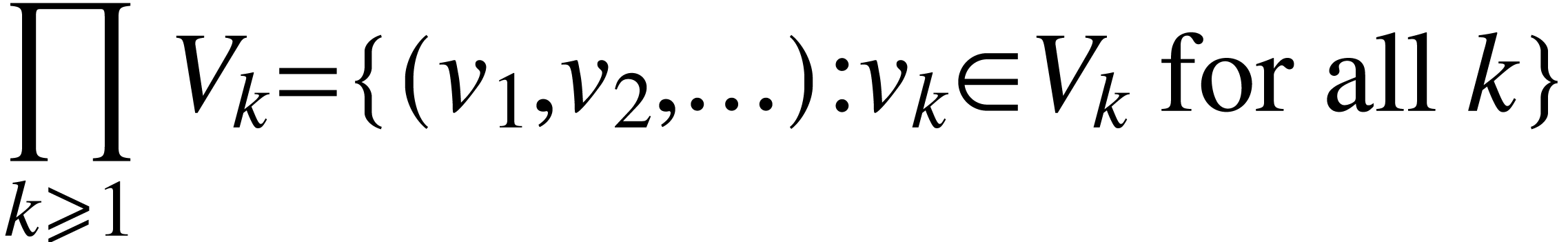
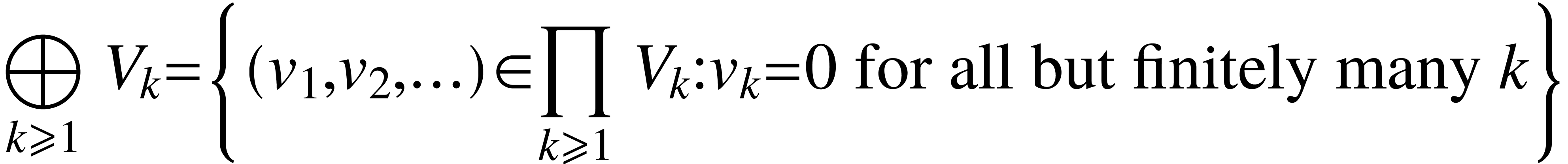
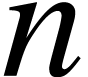 ,
,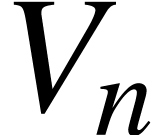 is a subspace of
is a subspace of 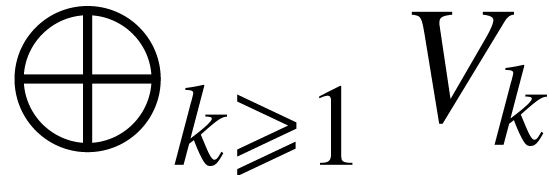 .
.